Расчёт полного теплового сопротивления
О расчёте статических потерь в силовой электронике написано не мало. Да и, казалось бы, для статичных процессов нет ничего сложного в расчёте. Но это на первый взгляд. На практике, когда требуется рассчитать допустимый ток нагрузки ключа, сталкиваешься с существенными трудностями. Из справочной информации легко можно дойти до теплового сопротивления радиатора силового модуля, но дальше возникают вопросы: как влияет тепловое сопротивление теплопроводной пасты, какая должна быть площадь охладителя и скорость обдува вентилятора, хватит ли площади станины, если используется не специальный охладитель… Всё это дополнительные тепловые сопротивления и дополнительный поправочные коэффициенты для допустимой мощности. О этих поправках и пойдёт речь ниже.
Если не брать в расчёт жидкостное охлаждение (которое, на практике, применяется крайне редко), то охлаждение – это всегда путь тепла от кристалла силового элемента до воздуха. Этот путь, представленный тепловыми сопротивлениями, схематично изображён на рисунке 1.
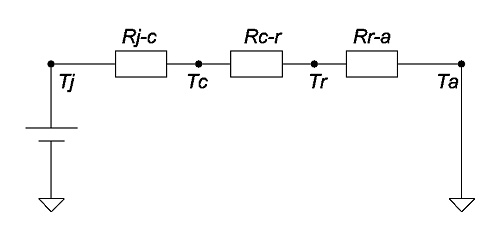
Rj-c – сопротивление кристалл-теплоотвод корпуса
Rc-r – сопротивление корпус-радиатор.
Rr-a – тепловое сопротивление радиатор-атмосфера.
Tj – температура перехода силового элемента;
Тс – температура теплоотвода корпуса;
Тr – температура радиатора (охладителя);
Та – температура окружающей среды.
Рисунок 1 – Эквивалентная схема теплового закона Ома
При расчёте предельно-допустимого тока модуля следует придерживаться следующей методики:
Тепловой закон Ома:
Tj = P х Rj-a + Ta.
Отсюда максимальная рассеиваемая мощность модуля: Р = (Tj – Та) / Rj-a
Здесь Tj – справочная величина для силового элемента (предельно-допустимое значение); Та – известная (или предполагаемая) температура окружающего воздуха, а вот величина Rj-a (суммарное тепловое сопротивлении кристалл – воздух) требует расчёта. Рассмотрим составляющие величины Rj-a в отдельности.
Rj-c. У всех уважающих себя производителей данный параметр указывается в документации. Зачастую приводится не только максимальное значение, но и типовое, хотя для расчётов рекомендуется брать всё-таки предельное значение.
Rc-r. Данное сопротивление практически полностью обусловлено качеством присоединения модуля к охладителю. Разумеется, при присоединении модуля все винты должны быть затянуты (и затянуты в правильном порядке), неплоскостность охладителя должна быть минимальна (в идеале - не более 30 мкм), шероховатость так же должна быть минимальна (не более 2,5 мкм). Но даже в таких идеальных условиях величина Rc-r не совсем понятна; необходим расчёт.
Тепловое сопротивление можно получить из коэффициента теплопроводности по формуле: Rc-r = h / (R х S)
Где h – толщина прокладки; R – тепловое сопротивление материала прокладки; S – площадь прокладки (площадь радиатора модуля).
В подавляющем большинстве случаев силовые модули ставятся на охладитель либо через силиконовую прокладку, либо через теплопроводную пасту. Для этих материалов: силиконовая прокладка имеет коэффициент теплопроводности 0,5…2 Вт/(м*К), паста КПТ-8 – 0,75 Вт/(м*К); прочие пасты, как правило, имеют коэффициенты от 0,5 до 3 Вт/(м*К). Толщина слоя пасты, в идеальном случае, должна составлять 0,02…0,05 мм, но допустим слой и до 0,1 мм. На практике, толщина слоя обычно составляет около 0,1 мм, а порою доходит и до 0,2…0,3 мм при значительной шероховатости или неплоскостности охладителя. Таким образом, для среднестатистического случая, т.е. для пасты КПТ-8 со слоем 0,1 мм получаем тепловое сопротивление 1 дм2 площади соприкосновения:
Rc-r = 0,0001 / ( 0,75 х 0,01 ) = 0,013 К/Вт или 13 К/кВт
Приведём самый худший (из предельно допустимого) вариант:
Rc-r = 0,0003 / ( 0,5 х 0,01 ) = 0,06 К/Вт или 60 К/кВт
Таким образом, в зависимости от типа пасты и её слоя тепловое сопротивление составляет от нескольких градусов до десятков градусов для 1 дм2 площади; средний случай – порядка 10…20 К/кВт на 1 дм2.
Для силиконовой прокладки цифры немного другие, обусловленные, в основном, толщиной прокладки. Толщина такого рода прокладок составляет, как правило, 0,15…2 мм; в большинстве случаев применяются прокладки толщиной 0,3 мм с теплопроводностью около 1 Вт/(м*К); тогда для площади 1 дм2:
Rc-r = 0,0003 / ( 1 х 0,01 ) = 0,03 К/Вт или 30 К/кВт
Для прокладки толщиной в 1…2 мм тепловое сопротивление может достигать нескольких градусов на Вт, а потому пренебрегать данным сопротивлением не стоит.
При использовании слюдяной прокладки необходимо учитывать, что с обеих её сторон так же следует наносить теплопроводную пасту с суммарной толщиной порядка тех же 0,1 мм.
Rr-a. Это сопротивление, прежде всего, зависит от площади охладителя и скорости потока воздуха. Разумеется, не маловажную роль здесь играет материал, из которого изготовлен охладитель, но, как правило, охладители изготавливаются из металлов, очень хорошо проводящих тепло и их сопротивлением, на фоне сопротивления воздуха, можно пренебречь.
Для специализированных охладителей производитель обязательно указывает тепловое сопротивление охладителя и зависимость данного параметра от скорости обдува. Здесь достаточно выбрать подходящий охладитель и необходимую рабочую точку. Немного сложнее, если в качестве охладителя выступает корпус прибора. Для металла коэффициент теплоотдачи составляет порядка 5…10 Вт/(м2*К) при естественной конвекции воздуха и порядка 50 Вт/(м2*К) при принудительном обдуве со скоростью 10…15 м/с. Это и есть исходные цифры для расчёта охлаждения через корпус. Проще говоря, если не применяется принудительное охлаждение, то 5…10 Вт передаваемой корпусу мощности приведут к нагреву площади 1 м2 на 1 К. Т.е. для 1 м2 плоской металлической поверхности тепловое сопротивление составляет 0,1…0,2 К/Вт (без принудительного обдува) и около 0,02 К/Вт при скорости обдува 10…15 м/с. Соответственно, для площади, например, 1 дм2 тепловое сопротивление будет составлять 10…20 К/Вт при естественной конвекции; аналогично для других площадей и скоростей обдува.
Приведём пример. Допустим, имеется задача: в приборе необходимо установить реле постоянного тока с рабочим напряжением 540 В и током нагрузки 80 А. Есть два варианта монтажа реле: либо непосредственно на корпус прибора через изолирующую прокладку, либо крепить к корпусу (так же через изоляторы) охладитель и уже на него устанавливать реле. Корпус прибора металлический с общей площадью 0,5 м2; установить вентилятор не представляется возможным; максимальная температура окружающей среды в процессе эксплуатации – 40 0С. Спрашивается: можно ли обойтись без охладителя?
Выбираем реле. Подходит реле МО15Д-120-12 (производства ЗАО «Электрум АВ»). Для данного реле напряжение насыщения коллектор-эмиттер (VCE(on)) составляет не более 3 В; тепловое сопротивление переход основание (Rth(j-с)) составляет не более 0,18 0С/Вт; максимальная температура перехода кристалла – 150 0С; площадь основания модуля – около 0,7 дм2.
Считаем мощность потерь: Р = 80 х 3 = 240 Вт.
Считаем полное тепловое сопротивление для случая установки реле на корпус через слюдяную прокладку толщиной 0,3 мм с двумя слоями пасты КПТ-8, каждый слой толщиной 100 мкм.
Rj-a = Rj-c + Rc-r + Rr-a = (0,18) + (2 х (0,0001 / ( 0,75 х 0,007 )) + 0,0003 / ( 1 х 0,007 )) + (0,2 / 0,5) = 0,66 К/Вт
Считаем максимальную рассеиваемую мощность данной конструкции для наших условий эксплуатации:
Р = (Tj – Та) / Rj-a = (150 – 40) / 0,66 = 166 Вт.
Аналогично считаем для охладителя Охл.153-250 так же производства ЗАО «Электрум АВ». Длинна охладителя 25 см; тепловое сопротивление – около 0,2 К/Вт.
Rj-a = (0,18) + (0,0001 / ( 0,75 х 0,007 )) + (0,2) = 0,4 К/Вт
Р = (150 – 40) / 0,4 = 275 Вт
Таким образом, устанавливать реле непосредственно на корпус через слюдяную прокладку нельзя, т.к. прибор перегреется. А вот установить реле на охладитель длинной 25 см можно, хотя и при этом варианте значительного запаса по температуре не получится.
Отсюда же, к слову сказать, можно подсчитать температуру не только охладителя, но и, например, корпуса модуля, а так же каких-то других частей конструкции участвующих в теплообмене. Приведённый метод расчёта является общепринятым, хотя и несколько упрощённым, однако, в подавляющем большинстве случаев, этого алгоритма более чем достаточно.

